1. 교류와 벡터
사인파 교류는 파형이나 식으로 표현할 수 있었지만, 크기와 방향을 갖는 벡터로도 표현할 수 있고, 교류를 취급하는 경우는 매우 편리하다. 그림 1-1은 사인파 교류의 묘사법을 보여 주고 있는데, 같은 그림 (a)에 있어서 𝑬𝒎, 𝑰𝒎과 같이 문자위에 • (도트)를 붙혀서 표현한다.
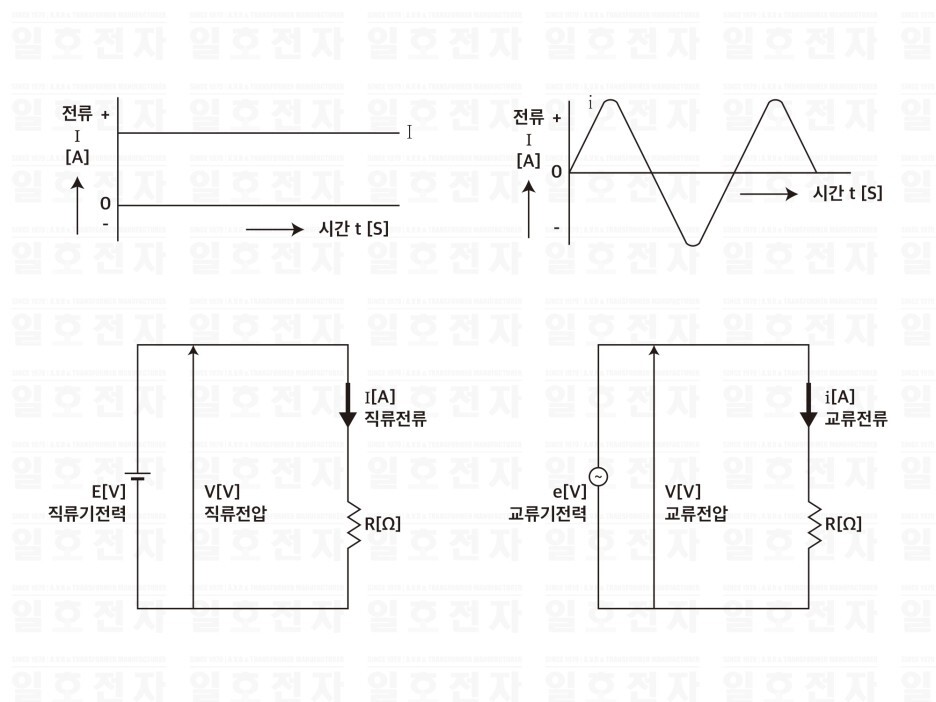
그림 1-1 회전 벡터
일반적으로, 교류의 크기는 실효치가 사용되고 있으므로, 사인파 교류와 회전 벡터와의 사이에 다음과 같은 약속을 한다.
벡터의 크기 = 사인파 교류의 실효치
벡터의 편각 = 사인파 교류의 위상각
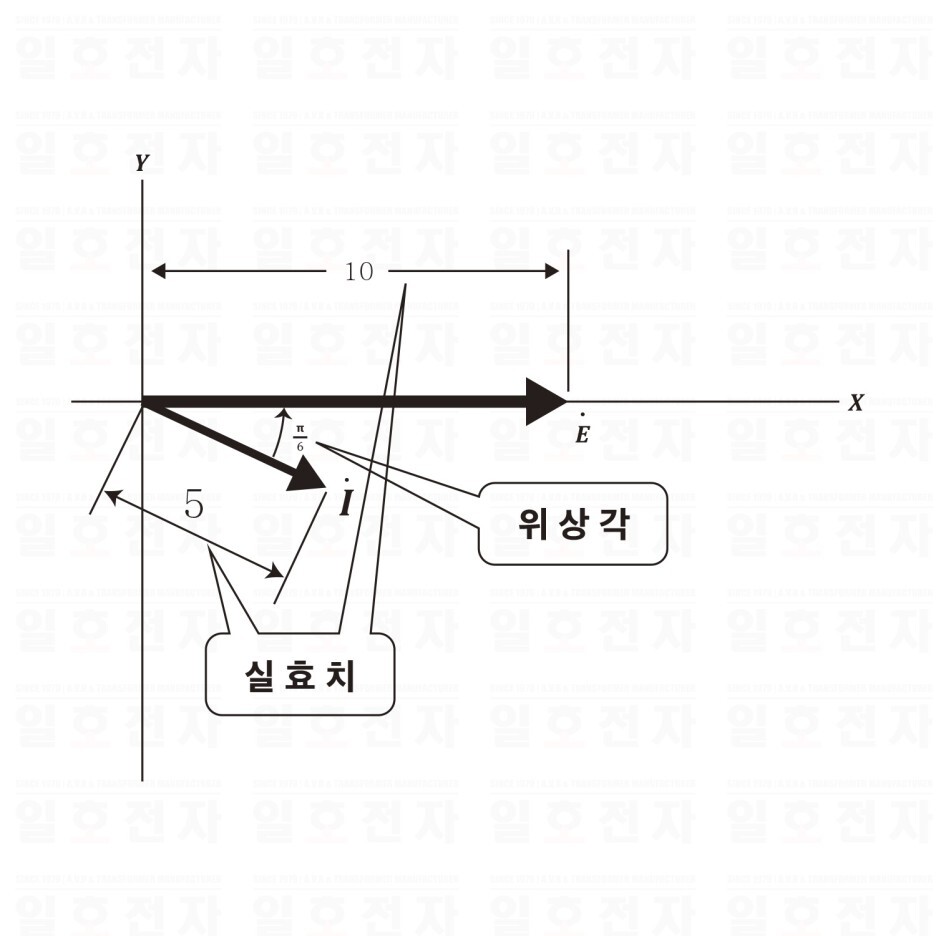
그림 1-2 벡터 그림의 예
예를 들면,
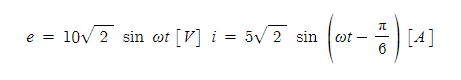
의 사인파 교류를 벡터로 표현하면
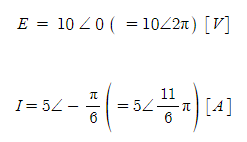
가 된다. 이들 벡터 그림은 그림 2-2과 같이 된다.
2. 벡터와 복소수
교류는 벡터로 표현할 수 있었으나, X축을 실부, Y축을 허부로 하는 복소수로 표현할 수 있다. 따라서 교류는 복소수로 표시할 수 있다.
(a) 복소수의 성질
실수와 허수의 합으로 표현되는 수를 복소수라고 한다.허수라는 것은 √-1, √-2, √-3 과 같은 수로, 허수 중 √-1을 허수 단위라고 하며, j라고 하는 기호로 표현한다. 즉, j = √-1이다. 따라서, j를 사용하면 모든 거기서, 복소수는 2개의 실수 a, b를 사용하여, 다음과 같이 표현된다. a + jb 이 a를 복소수의 실부, b를 허부라고 한다.
(b) 벡터와 복소수
그림 2-3와 같이 전류 벡터 𝑰는 직각 좌표의 X축에 실부, Y축에 허부를 눈금으로 하면 복소수와 대응시킬 수 있고, 복소수로 다음과 같이 표현할 수 있다.
𝑰=𝑰1 + 𝒋𝑰2
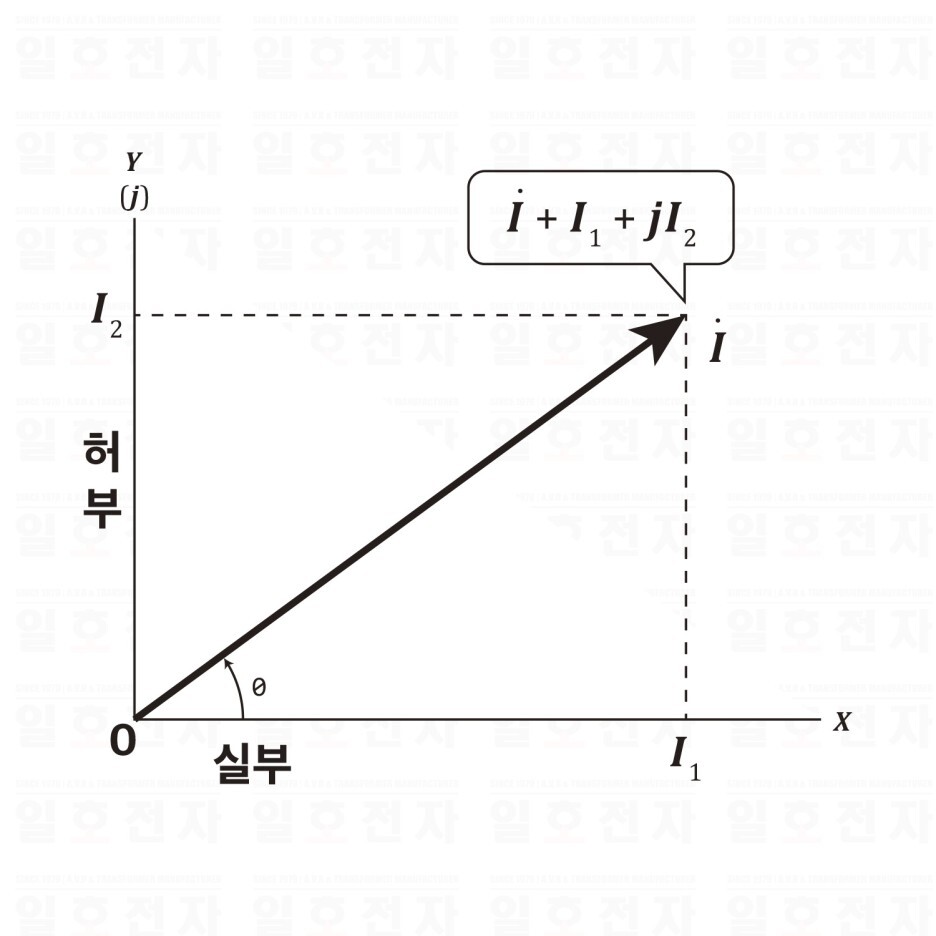
그림 1-3 벡터와 복소수
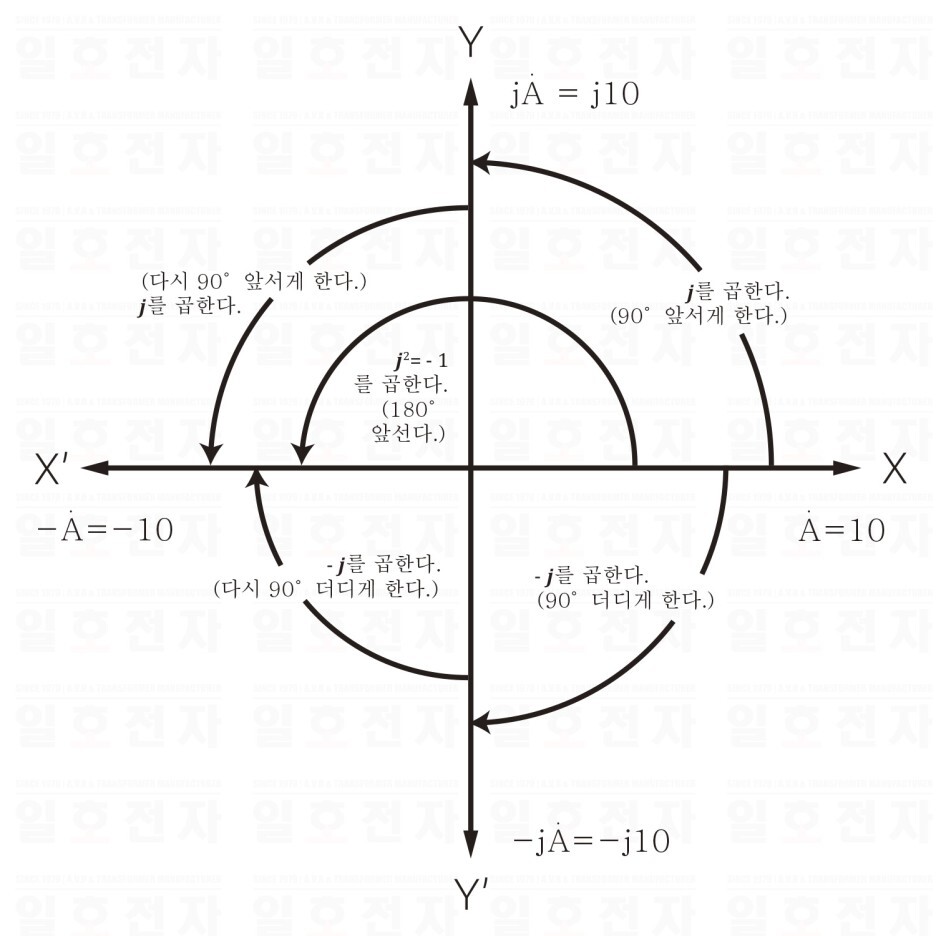
그림 1-4 벡터와 j
여기에서 벡터 𝑰가 복소수로 표현되는 때도 𝑰와 같이 도트표(•)를 붙여서, 복소수라고 하는 것을 나타낸다. 𝑰의 크기 (절대치) 𝑰와 위상각(편각) θ는 다음과 같이 구하여진다.
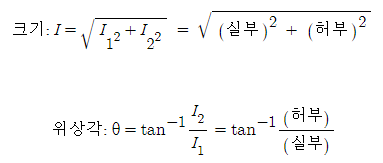
이상과 같이 전류 등의 벡터를 복소수로 표현하고, 이것들을 사용해 교류 회로를 계산하는 방법을 기호법이라고 한다. 또한 그림 2-4는 벡터 𝑨에 𝑱나 -𝑱를 곱함으로써, 위상을 90° (𝝿/2 [rad]) 앞서게 하거나, 더디게 할 수 있는 것을 표현하고 있다.
3. 저항뿐인 교류회로
그림 1-5는 저항 𝑹[Ω]에 교류 전압 𝒗[V]를 더한 회로이다. 지금, 교류 전압 𝒗를
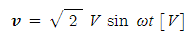
(1·1)
라고 하면, 저항에 흐르는 전류 𝒊𝑹은 옴의 법칙에 따라 다음과 같이 된다.
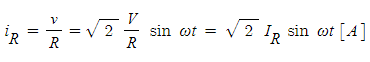
(1·2)
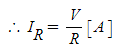
(1·3)
식 (1·1)(1·2)를 파형과 벡터로 표현하면, 그림 1-6, 1-7과 같이 된다.
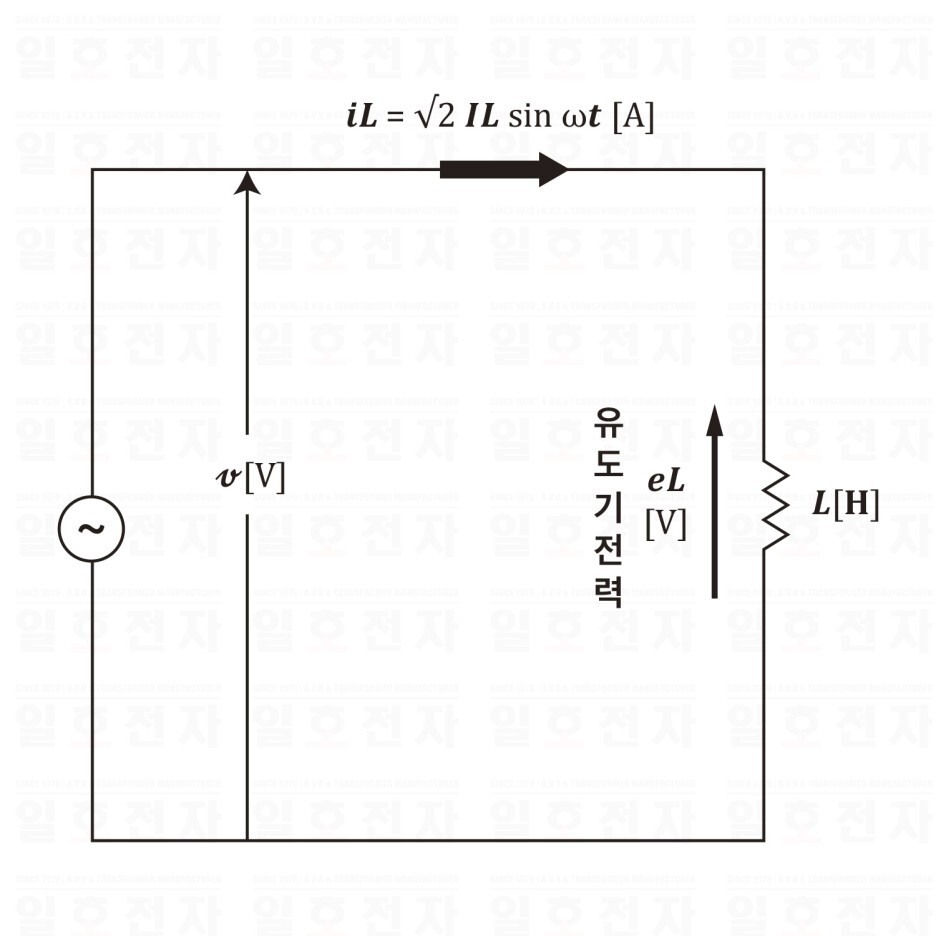
그림 1-5 저항만의 회로
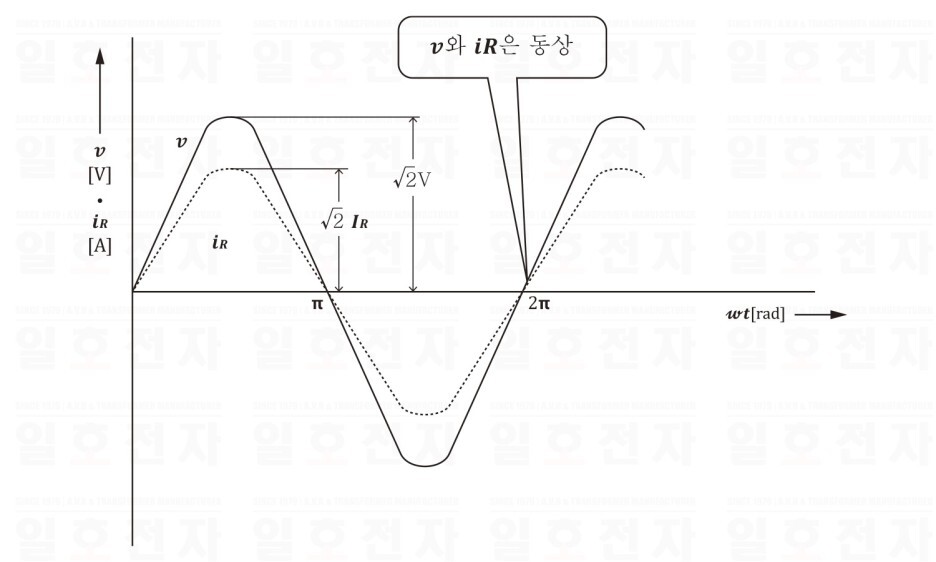
그림 1-6 전압과 전류의 파형
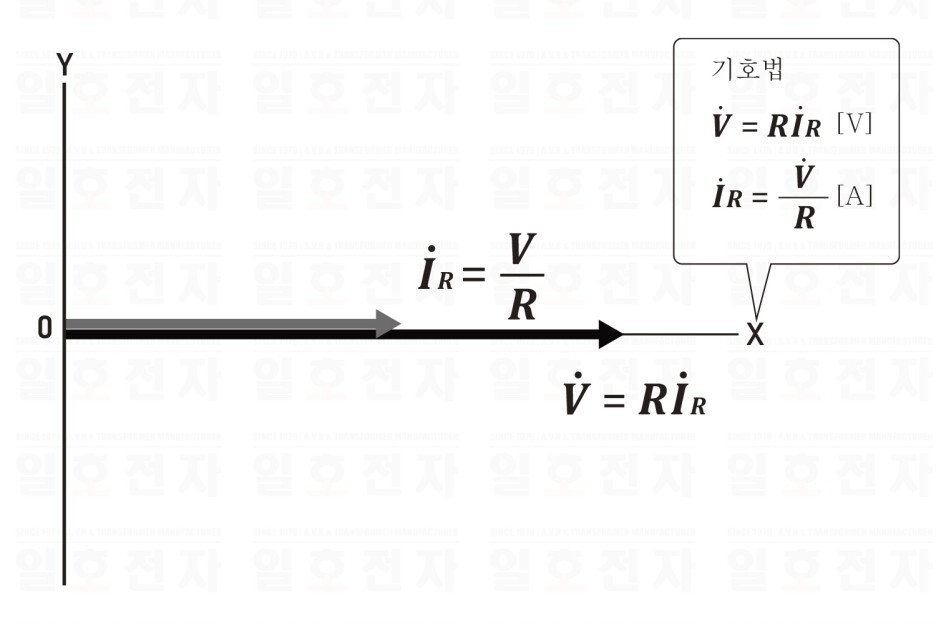
그림 1-7 저항 회로의 전압과 전류의 벡터 그림
4. 코일뿐인 교류회로
그림 1-8은 인덕턴스 𝑳[𝐇]를 갖는 코일에 교류 전압 𝒗[V]를 더한 회로이다.
여기에서 코일의 유도 기전력 𝐞𝑳은 다음과 같이 된다.
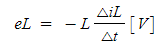
(1·4)
그런데, 그림 1-8에서 코일에 교류 전압 𝒗을 더하여
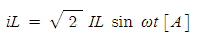
(1·5)
의 전류를 흐르게 했다고 하면, 유도 기전력 𝒆𝑳은 식 (1·4),(1·5)에서
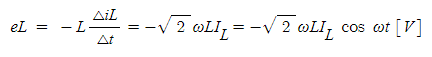
여기에서 전원의 전압 𝒗는 유도 기전력 𝒆𝑳과 크기 같고, 방향이 역의 전압이므로
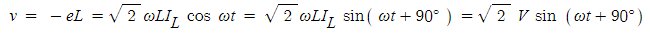
(1·6)
식 (1·6)에서 전압과 전류의 실효치는
𝑽=ω𝑳𝑰𝑳 [V]
(1·7)
또한, ω𝑳 = 𝑿𝑳 로 놓고, 식 (1·7)을 변형하면,
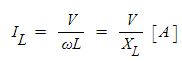
(1·8)
이 된다. 𝑿𝑳 은 교류 전류의 흐름을 방해하는 코일의 작용을 표현하고, 이 𝑿𝑳 을 유도 리액턴스라고 부르며, 단위에는 Ω를 사용한다. 또한, 𝑿𝑳 은 주파수와의 관계를 사용하면 다음과 같이 표현할 수 있다.
𝑿𝑳 = ω𝑳 = 2𝝿⨍𝑳 [Ω]
(1·9)
따라서, 유도 리액턴스 𝑿𝑳은 주파수 f[Hz]에 비례한다.
그리고, 식 (1·5),(1·6)에서 교류 전류 𝒊𝑳을 기준으로 한다면, 교류전압 𝒗의 위상은 전류 𝒊𝑳보다 90° 앞선 것을 알 수 있다. 그림 1-9, 1-10은 각 각의 파형과 벡터 그림이다.
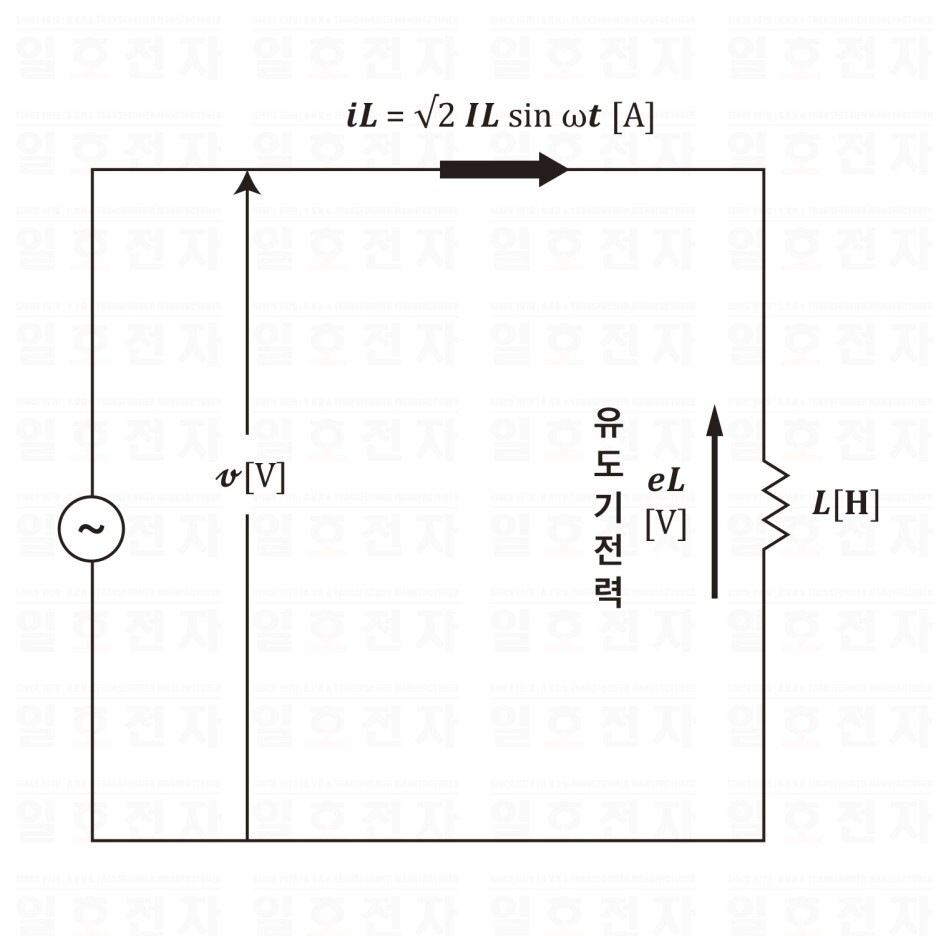
그림 1-8 코일뿐인 회로
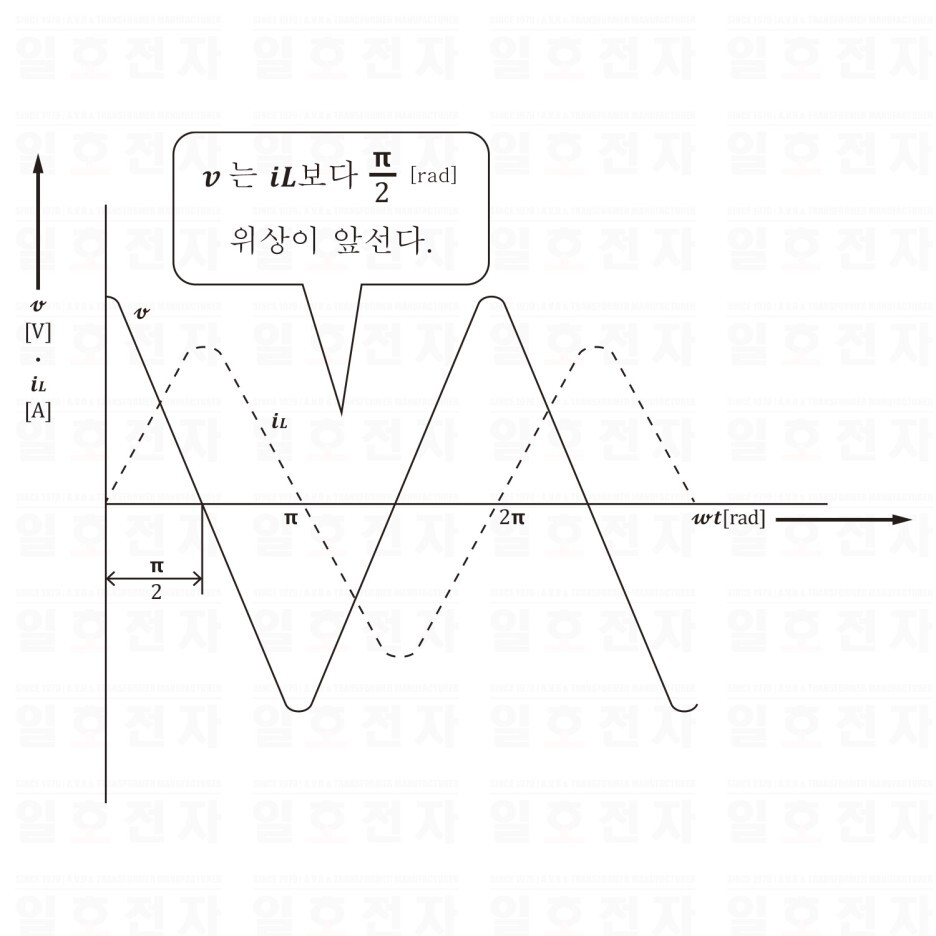
그림 1-9 전압과 전류의 파형
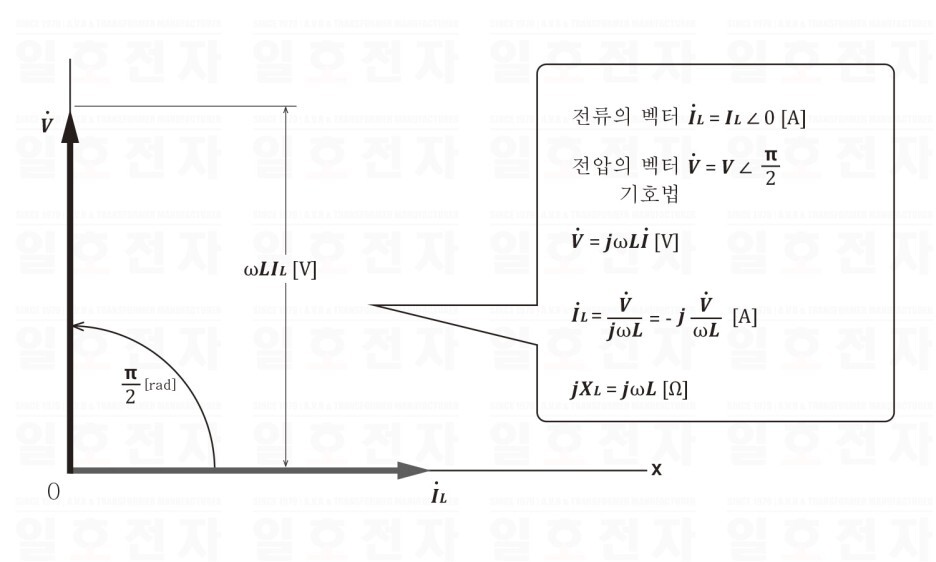
그림 1-10 코일뿐인 전류와 전압 벡터
5. 콘덴서 뿐인 교류 회로
그림 1-11은 정전 용량 C[F]를 가진 콘덴서에, 교류 전압 𝒗[V]를 더한 회로이다. 지금 이 그림과 같이 콘덴서에 가하는 전원의 전압을
𝒗=√2 V sin ω𝒕 [V]
로 하면, 콘덴서에 저장되는 전하 𝓺는 𝓺=𝑪𝒗[C]이므로
𝓺=√2 CV sin ω𝒕 [V]
(1·10)
이 때, 콘덴서에 흐르는 전류 𝒊𝒄는 전하 𝓺의 시간적인 변화의 비율로 정해지고
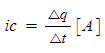
(1·11)
가 된다. 식 (1·10),(1·11)에서
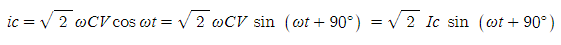
(1·12)
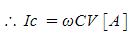
(1·13)
또한, ωC = 1/Xc로 하고 식 (1·13)을 변형하면
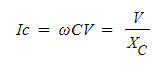
(1·14)
가 된다.
Xc는 교류 전류를 방해하는 콘덴서의 작용을 표현하고, 이 Xc를 용량 리액턴스라고 하며, 단위는 Ω를 사용한다. 또한 Xc는 주파수와의 관계를 사용하면, 다음과 같이 표현할 수 있다.
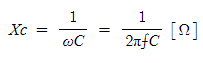
(1·15)
이와 같이 용량 리액턴스 Xc는 주파수 f[Hz]에 반비례한다. 그림 1-12, 그림 1-13은 전압, 전류의 파형과 벡터 그림이다.
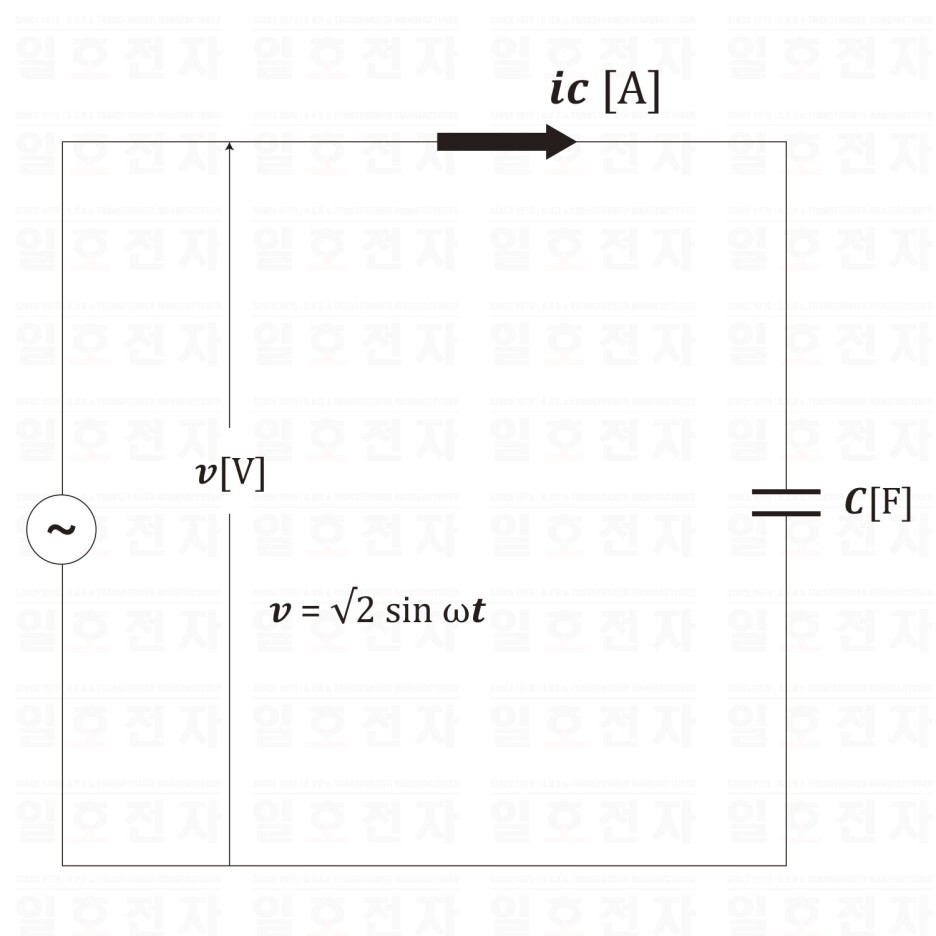
그림 1-11 콘덴서뿐인 회로
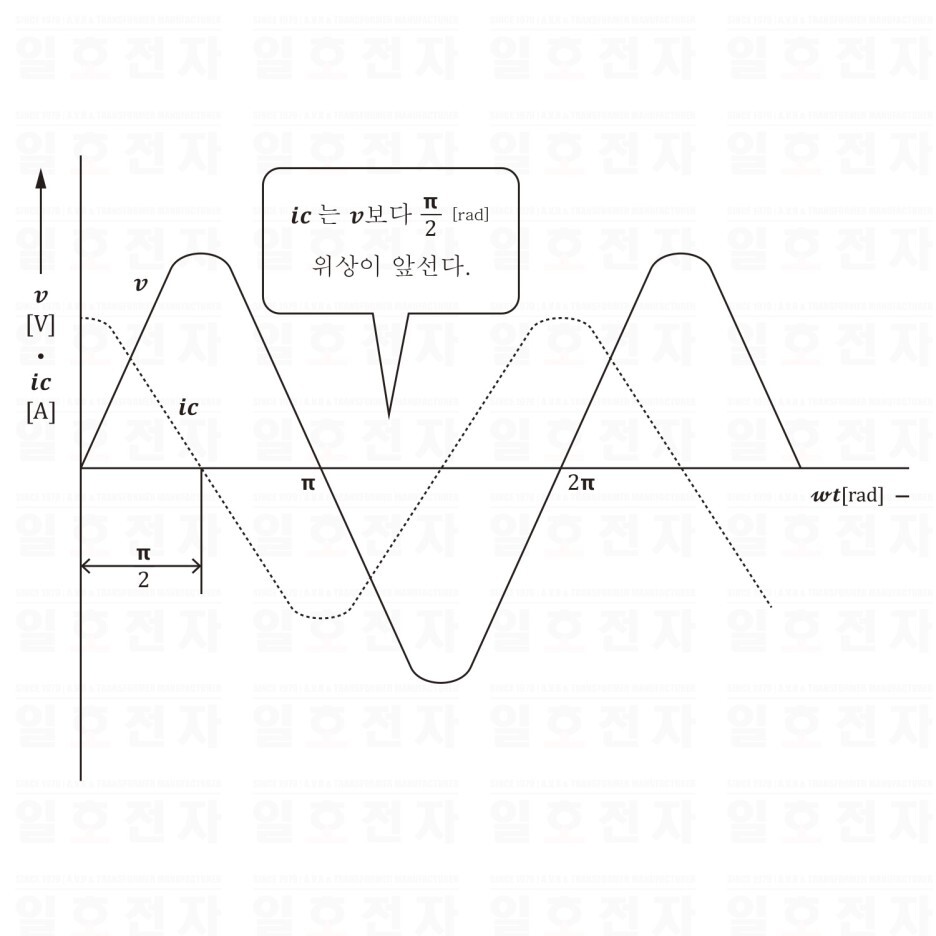
그림 1-12 전압과 전류의 파형
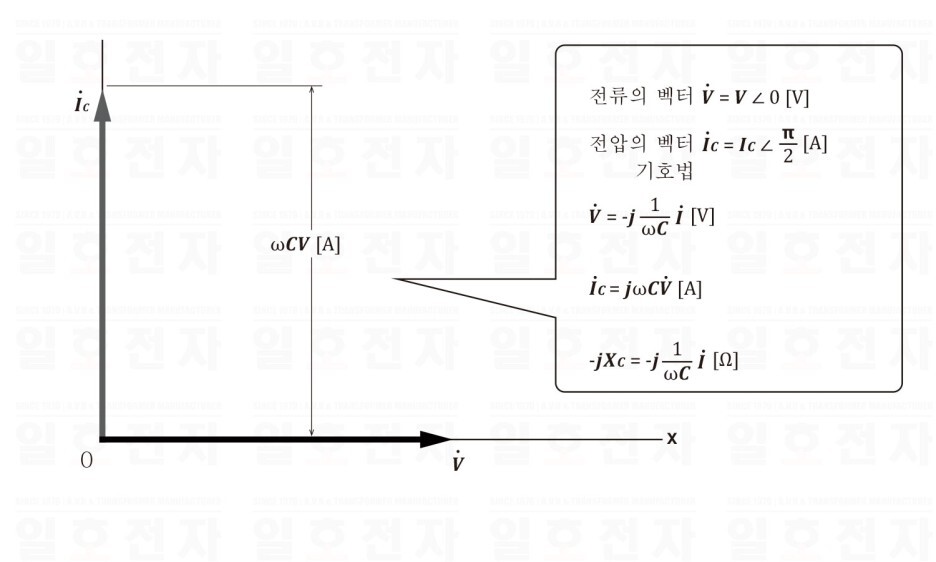
그림 1-13 콘덴서뿐인 전압과 전류의 벡터 그림
'전기 전자의 기초 > 전자 회로의 이해하기 위한 교류 회로' 카테고리의 다른 글
| 2-1 교류의 표현법 (0) | 2022.06.28 |
|---|