1. 교류라는 것은
그림 1-1(a)와 같이 직류는 시간이 경과하더라도 크기와 방향은 일정한데, 그림 1-1(b)와 같이 교류는 시간과 함께 크기와 방향이 주기적으로 변화한다.
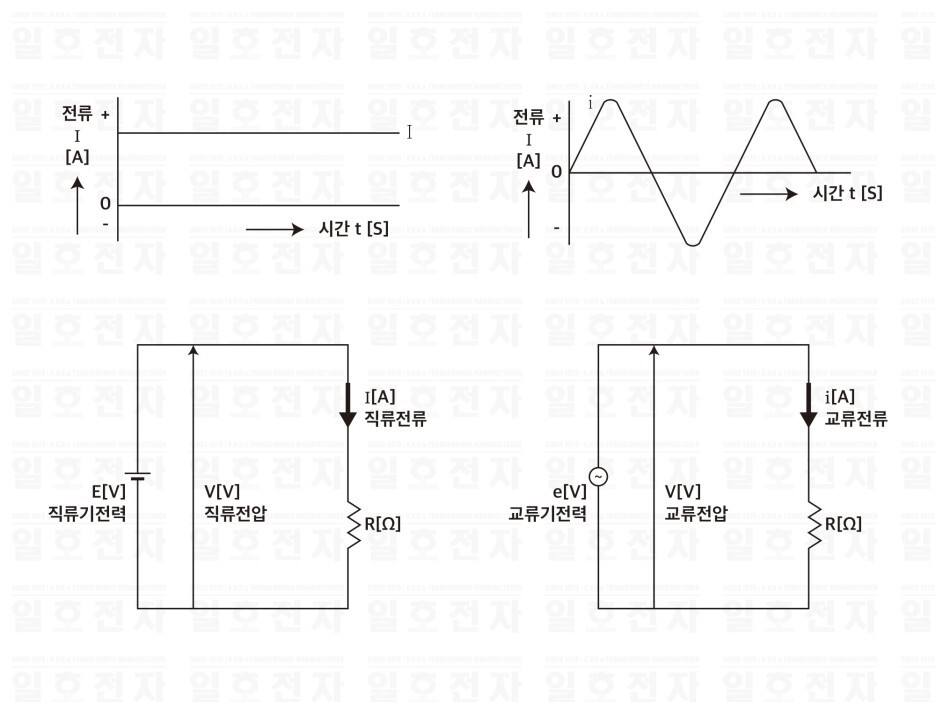
그림 1-1 직류와 교류
2. 사 인 파 교 류
그림 1-1(b)와 같은 교류의 파형은 사인 곡선이기 때문에, 사인파 교류라고 불려진다. 일반적으로, 단순히 교류라고 하면 사인파 교류를 뜻한다. 그림 1-2는 사인파의 묘사법으로 반지름을 선분 OP로 하여, OX의 위치에서 반 시계 방향에 일정한 속도로 회전하고, 회전축 θ를 횡축에, 그 때의 수직선의 길이 PQ를 종축에 잡고, 매끈한 곡선으로 연결해 가면 된다. 이 경우, 각 각의 각도의 장소에서 얻을 수 있는 수직선의 길이 PQ는 다음과 같이 된다.
PQ=OP sin θ
다음에 사인파 교류 전압을 발생하는 것으로 교류 발전기가 있다. 그림 1-3은 그 원리 그림이고, 자석의 N극과 S극 사이에 놓인 코일이 일정한 속도로 1회전할 때에 발생하는 기전력을 표시한 것이다.
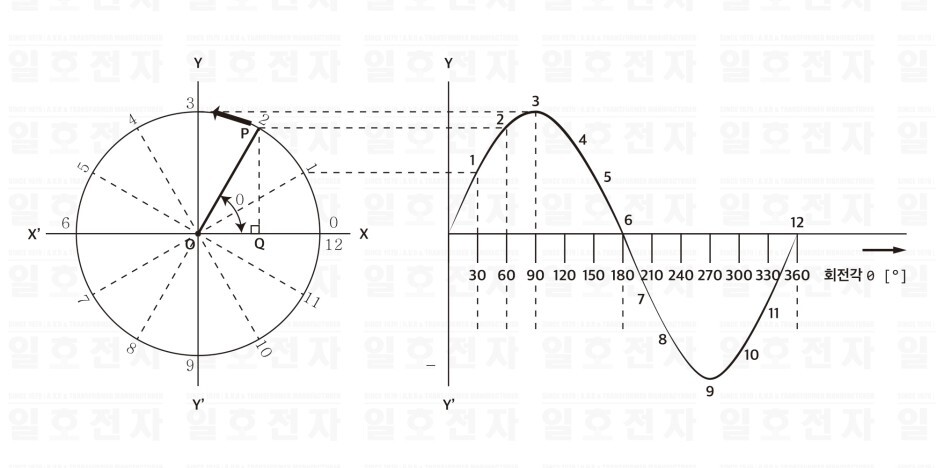
그림 1-2 사인파의 묘사법
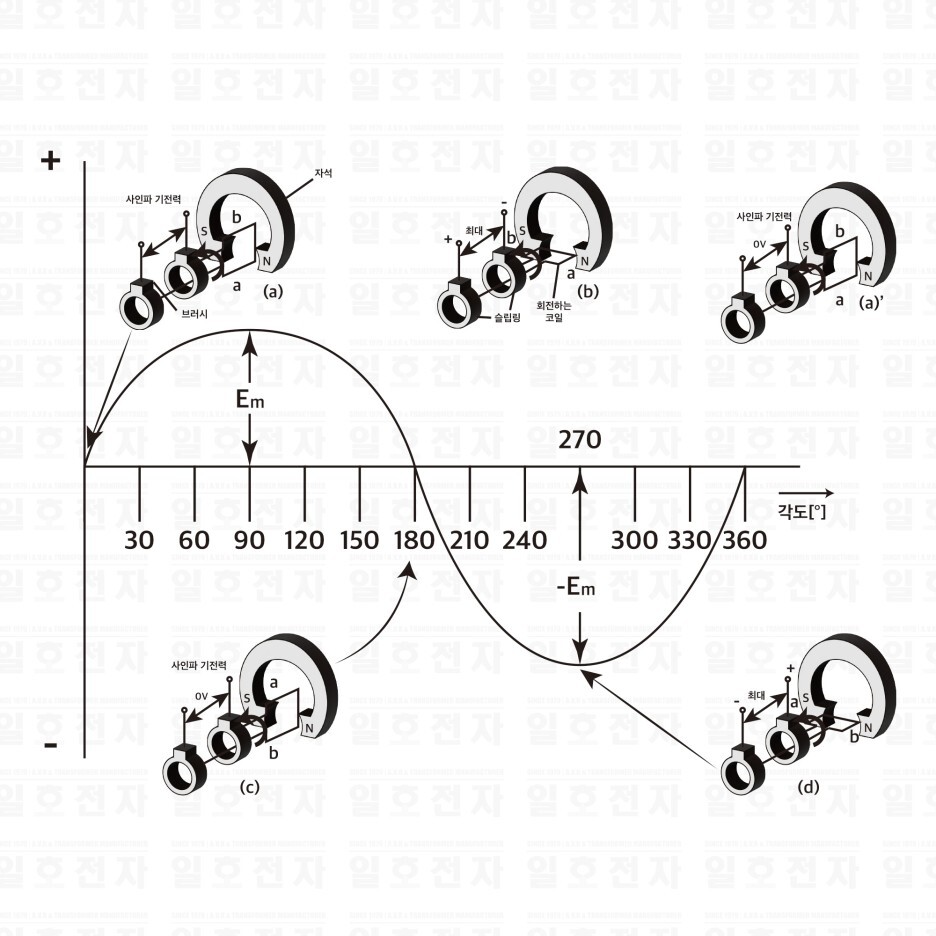
그림 1-3 사인파 기전력의 발생.
이 경우, 각 각의 각도로 얻을 수 있는 기전력 e는 다음과 같이 된다.
e = Em sin θ [V]
여기에서, sin θ의 θ는 각을 [°]로 표시하고 있는데, 각을 원의 주위의 길이, 즉, 호의 길이를 이용하여 표현하는 호도법이라고 하는 것이 있다. 호도법으로 표시한 각의 단위를 라디안[rad]이라고 하고, 사인파 교류를 식으로 표시하기도 하는데, 작도나 계산에 편리하다. (그림 1-4 참조) 또한, 1초간에 몇 라디안 회전하였는가라고 하는 각도의 크기를 각속도라고 하며, 단위는 rad/s를 사용한다. 거기서, 각 속도를 𝔀[rad/s]로 하고, 𝒕[𝒔]간에 θ[rad]만 회전했다고 하면, 회전각 θ는 다음과 같이 된다.
θ=𝔀𝒕 [rad]
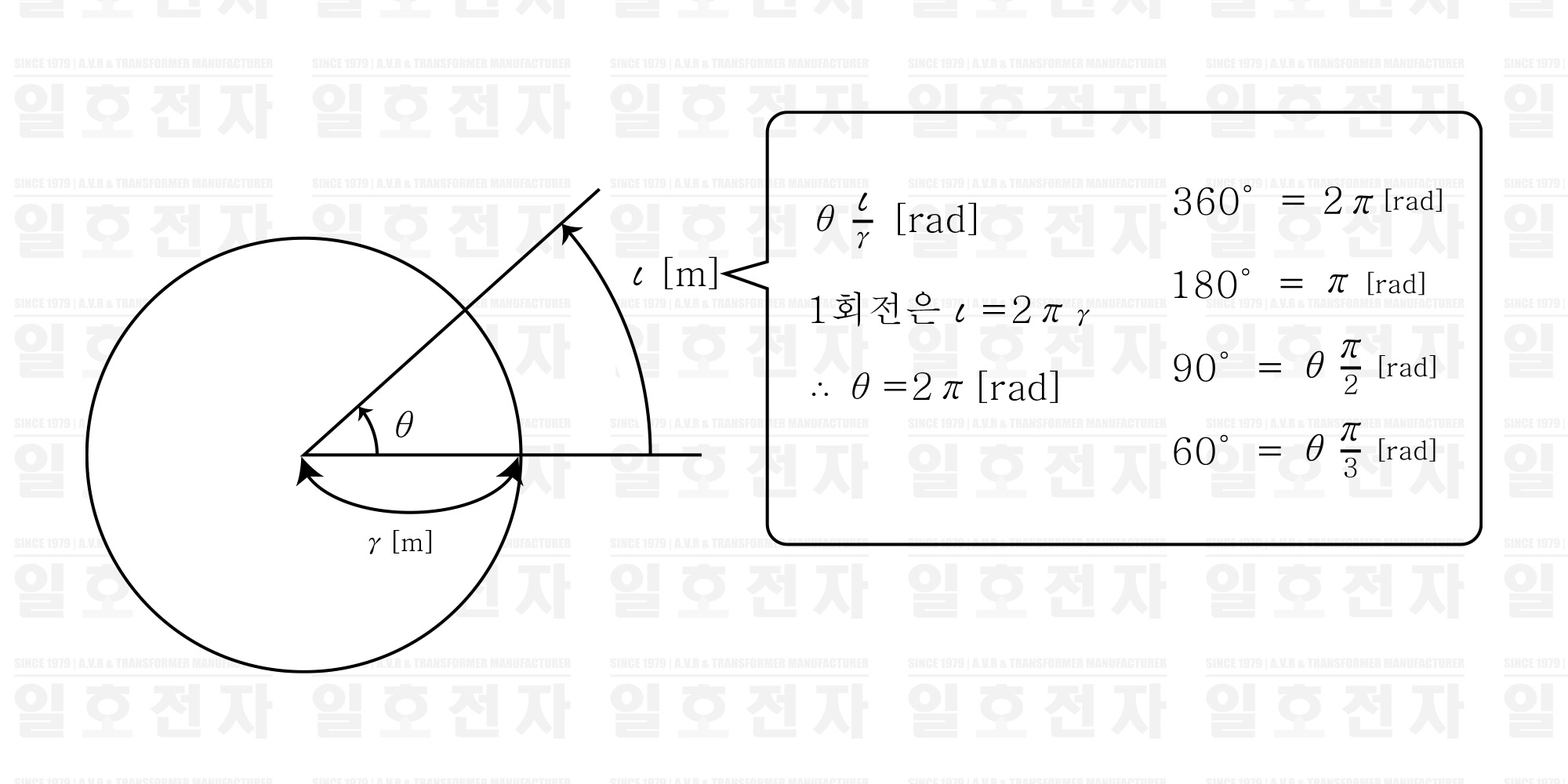
그림 1-4 호도법
3. 주파수와 주기
그림1-3에 있어서, 코일이 일정한 각 속도로 1회전하면 교류 기전력은 0, 𝑬𝒎, 0, -𝑬𝒎, 0 과 1개의 파가 발생하며, 이것을 1사이클이라고 한다. 그림 1-5와 같이 코일이 1초간에 50회 회전하면, 1초간에 50사이클의 파형이 생긴다. 이와 같은 1초간 당의 사이클수를 주파수라고 하고, ⨍로 표현하고, 단위에는 헤르쯔 [Hz]를 사용한다. 이 경우 ⨍=50Hz가 된다.
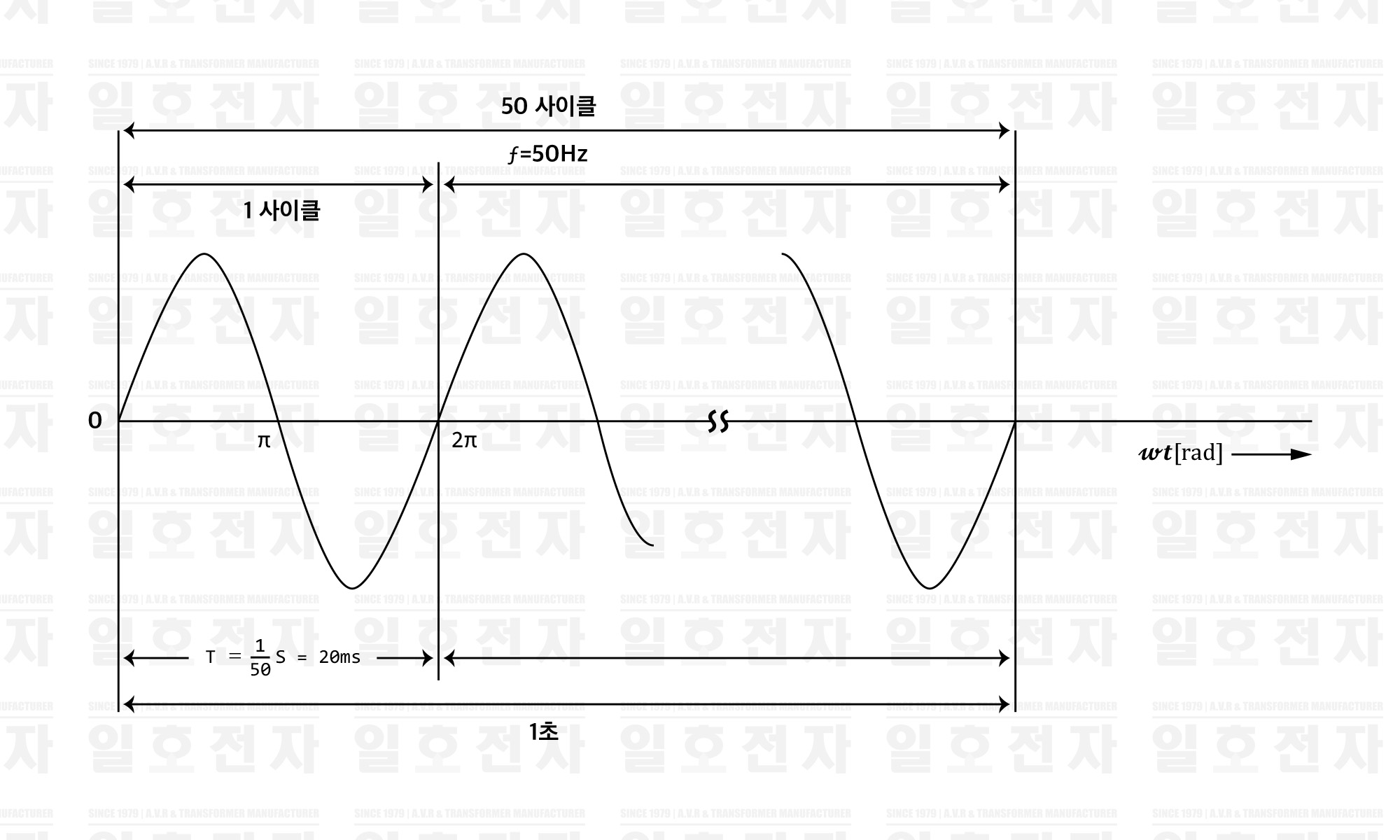
표 1-5 주파수와 주기
또한, 주파수 ⨍[Hz]의 교류에 있어서, 코일은 1초간에 2𝝿⨍[rad] 회전하게 된다. 따라서, 𝒕초간 코일이 회전하였다고 하면, 2𝝿⨍𝒕[rad]가 되고, 각과 시간의 관계는 다음과 같이 된다.
θ = 2𝝿⨍𝒕 [rad]
여기에서, θ = 𝔀𝒕 [rad] 이기 때문에, 𝔀는 다음과 같이 된다.
𝔀=2𝝿⨍[rad/s] 이 ω를 각 주파수라고도 한다.
그런데, 교류 파형의 하나의 되풀이에 필요한 시간을 주기라고 하며, 𝑻로 표현하고 단위로는 초 [s]를 사용한다. 주파수 ⨍[Hz]의 교류에서는 1초간에 ⨍회의 파형이 되풀이하므로, 1회당 시간은 1/⨍[s]이다. 따라서, 주기 𝑻와 주파수 ⨍사이에는 다음 식이 성립한다.
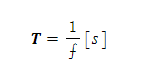
또한, 주파수나 주기의 단위는 보통 아래 단위를 사용한다.
주 파 수
1kHz (킬로헤르쯔) = 103Hz
1MHz (메가헤르쯔) = 106Hz
1GHz (기가헤르쯔) = 109Hz
1THz (테라헤르쯔) = 1012Hz
주 기
1ms (밀 리 초) = 10-3s
1μs (마이크로초) = 10-6s
1ns (나 노 초) = 10-9s
그림 1-3의 교류기 전력의 식
𝒆 = 𝑬𝒎 𝒔𝒊𝒏 θ [𝗩]
𝒆 = 𝑬𝒎 𝒔𝒊𝒏 𝔀𝒕 θ [𝗩]
𝒆 = 𝑬𝒎 𝒔𝒊𝒏 2𝝿⨍𝒕 [𝗩]
4. 순간치와 최대치
교류 기전력 𝒆는 다음 식과 같이 표현되고, 또한 그림 1-6과 같이 그릴 수 있다.
𝒆 = 𝑬𝒎 𝒔𝒊𝒏 θ [𝗩]
윗식 및 그림 2-6에서 기전력 𝒆의 값은 𝒆1, 𝒆2, 𝒆3와 같이 시간적으로 변화하고있고, 이 순시에 있어서의 값을 순시치라고 한다. 순시치 중, 최대의 값 𝑬𝒎을 최대치 (𝑬의 𝒎은 𝒎𝒂𝒙𝒊𝒎𝒖𝒎 : 최대) 또는 진폭이라고 한다. 또한, 파형의 산꼭대기와 골짜기의 밑바닥 사이의 값을 피크 투 피크 (𝑬𝒑𝒑)값이라고 한다. 또한, 교류 전류의 경우는 각 각을 𝑰𝒎, 𝑰𝒑-𝒑로 표현한다.
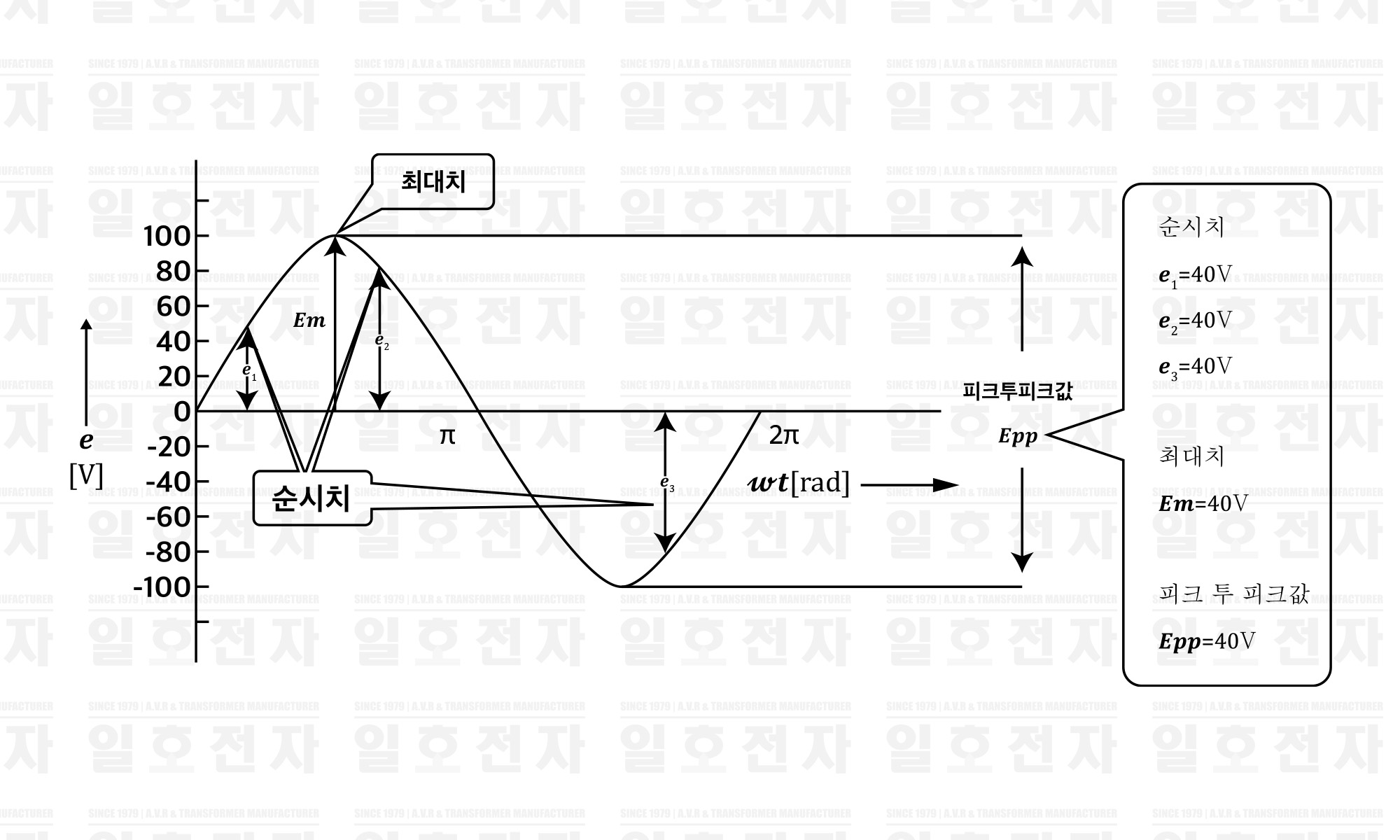
표 1-6 순시치와 최대치
5. 평 균 치
사인파 교류의 파형은 음양이 대칭이기 때문에, 평균하면 0이 된다. 그래서, 그림 1-7과 같이 교류 파형의 0으로부터 𝝿[rad]까지의 양의 기간에 대해서 평균을 취한다. 이 평균을 취한 높이를 평균치라고 하고, 𝑬𝒂𝒗로 표현한다. (𝒂𝒗는 𝒂𝒗𝒆𝒓𝒆𝒊𝒈𝒆 : 평균) 또한, 교류 전류의 경우는 𝑰𝒂𝒗으로 표현한다. 평균치와 최대치 사이에는 다음 관계가 있다.
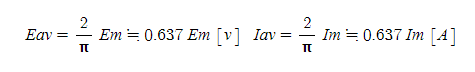
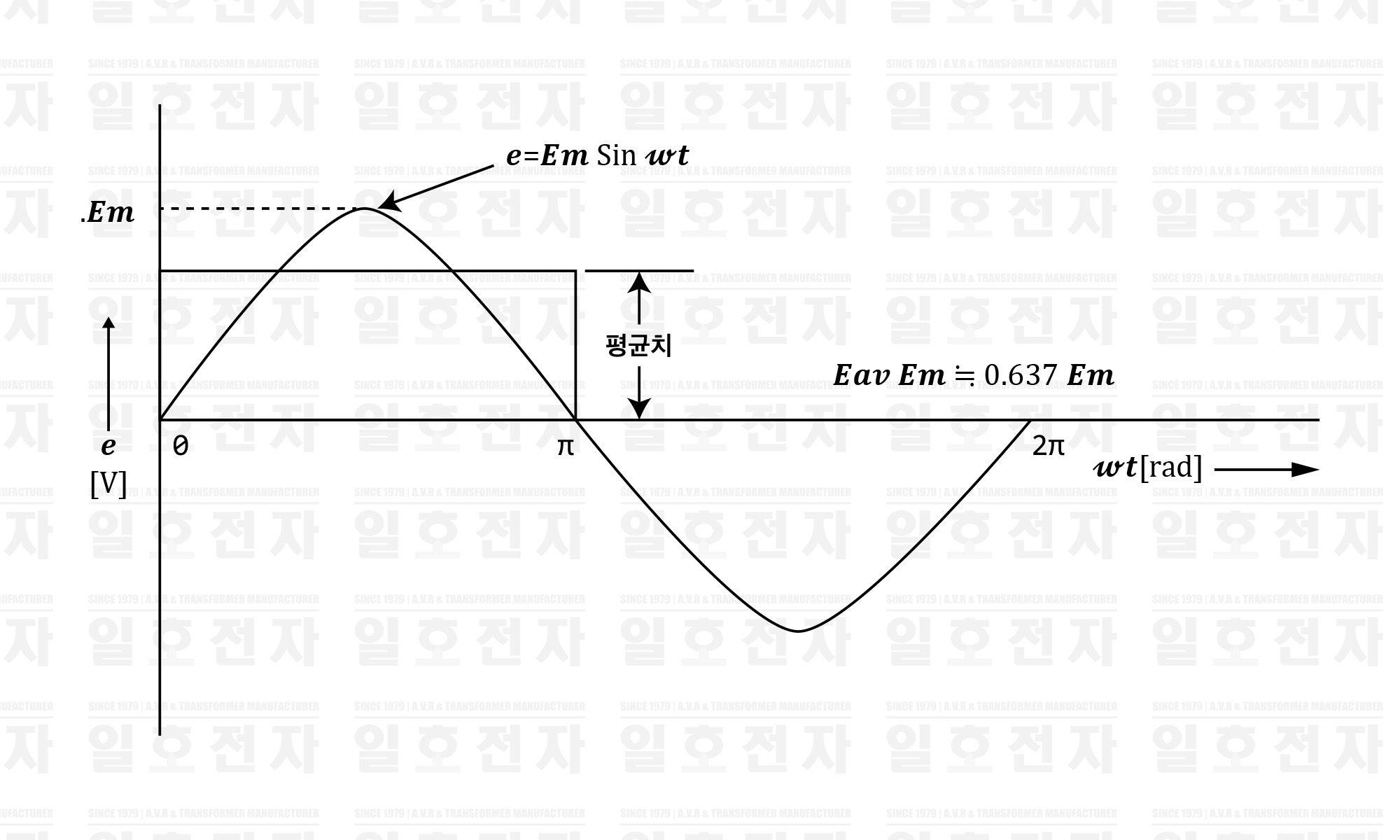
표 1-7 평균치
6. 실 효 치
그림 1-8(a),(b)와 같이 동일 저항 𝑹[Ω]에 직류 기전력과 교류 기전력을 더하면 저항은 발열한다. 이 때, 저항의 발생 열량이 서로 동등하면, 직류 기전력 𝑬[𝑽]와 교류 기전력 𝒆 [𝑽]는 동일 효과가 있다고 고려되며, 실제로 효과가 있는 값이라는 점으로, 이 𝑬[𝑽]를 교류 기전력 𝒆 [𝑽]의 실효치라고 한다. 교류의 크기를 표현하는 데는 보통 실효치가 많이 사용되고, 실효치와의 사이에는 다음 관계가 있다.
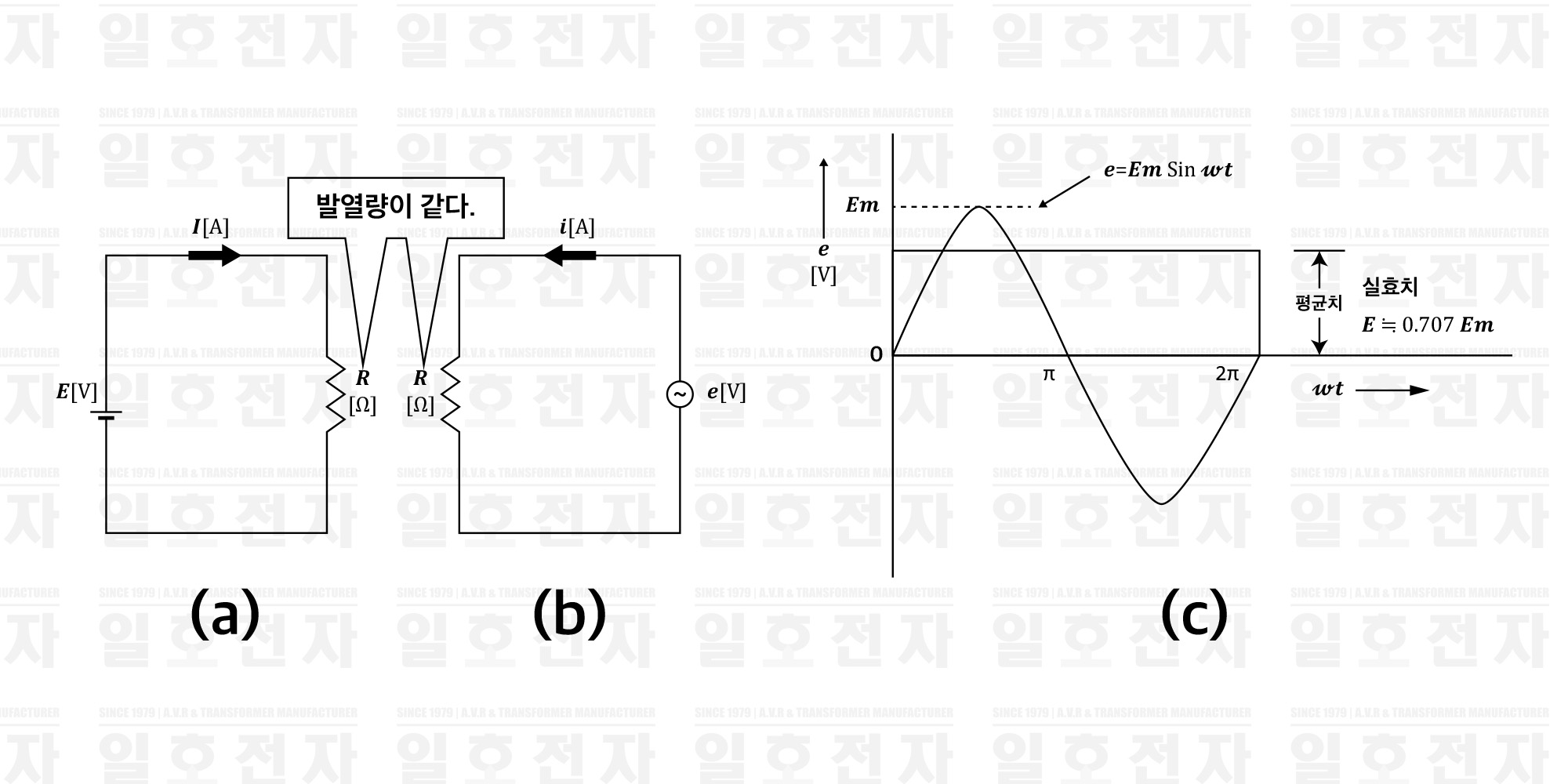
표 1-8 실효치
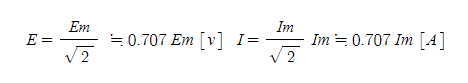
7. 위 상
그림 2-9(a)와 같이 A코일에 대해서 B코일을 90° 만 뒤에 비키어 놓고, 자계 중에서 함께 회전시키면, 같은 그림 (b)와 같이 각 기전력이 발생한다. 즉, 𝒆𝑩는 𝒆𝑨 보다 90° 더디게 𝒆𝑨와 같이 변화한다. 이 때, 𝒆𝑨와 𝒆𝑩와의 사이에는 90°의 위상차가 있다고 하고, 𝒆𝑩는 𝒆𝑨보다 위상이 더딘다고 말한다. 여기에서 𝒆𝑨를 기준으로서 𝒆𝑩를 표현하면, 다음과 같이 된다.
𝒆𝑨 = 𝑬𝒎 𝐬𝐢𝐧 ω𝒕 [V] 𝒆𝑩 = 𝑬𝒎 𝐬𝐢𝐧 (ω𝒕 - θ) [V]
또한, 2개의 코일에 위상차가 없는 경우, 또는 360°의 위상차, 360°의 배수의 위상차의 경우를 동상이라고 한다.
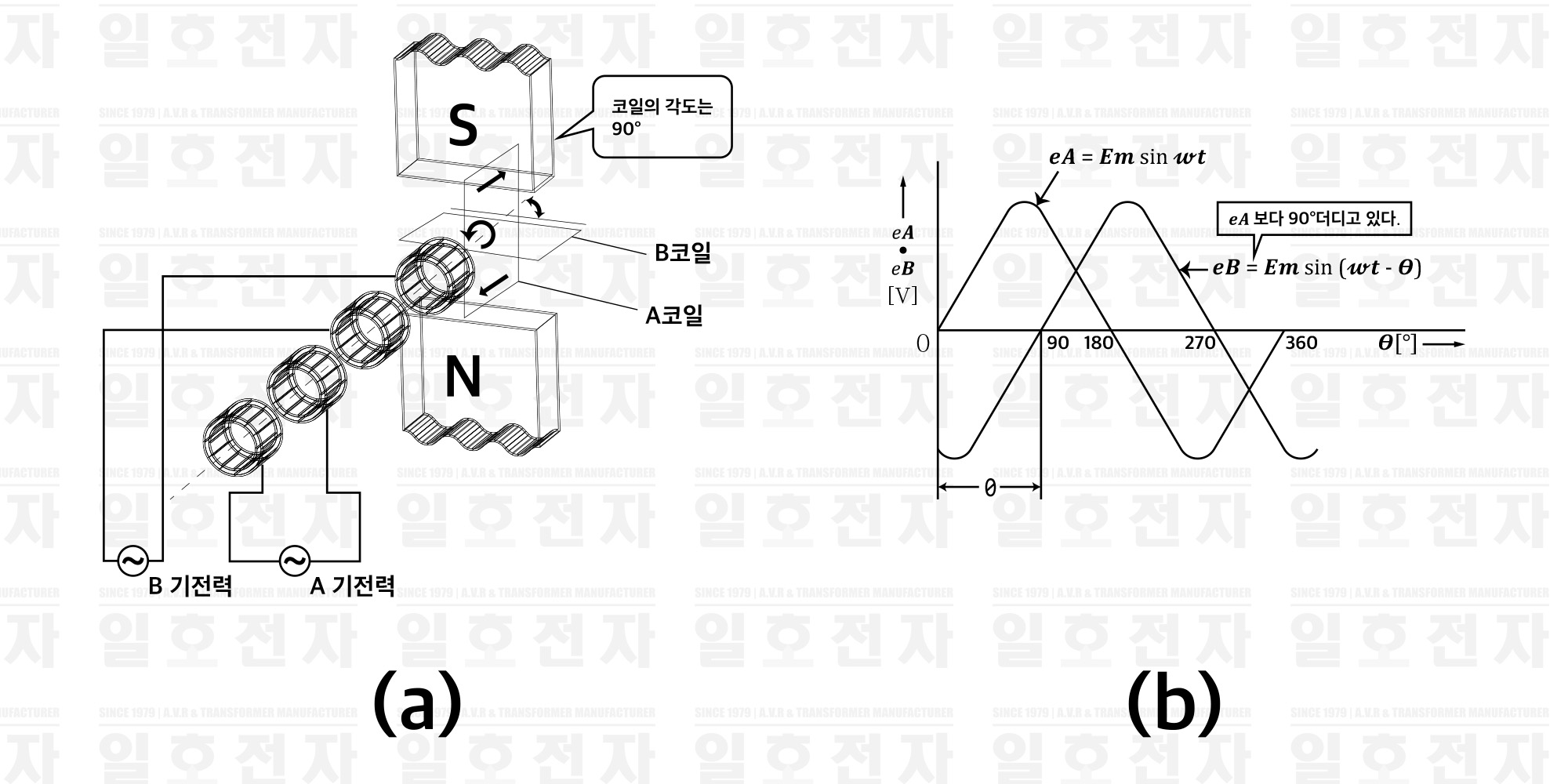
표 1-9 위 상
'전기 전자의 기초 > 전자 회로의 이해하기 위한 교류 회로' 카테고리의 다른 글
| 2-2 교류가 R, L, C에 가해지면 (0) | 2022.07.13 |
|---|