일호전자

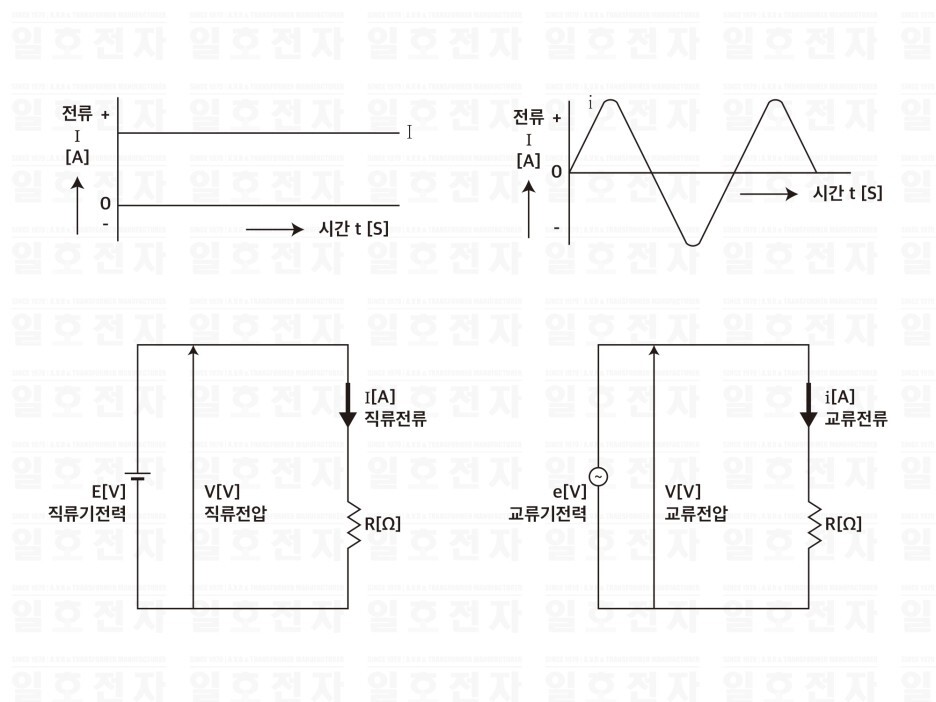
1. 교류와 벡터 사인파 교류는 파형이나 식으로 표현할 수 있었지만, 크기와 방향을 갖는 벡터로도 표현할 수 있고, 교류를 취급하는 경우는 매우 편리하다. 그림 1-1은 사인파 교류의 묘사법을 보여 주고 있는데, 같은 그림 (a)에 있어서 𝑬𝒎, 𝑰𝒎과 같이 문자위에 • (도트)를 붙혀서 표현한다. 그림 1-1 회전 벡터 일반적으로, 교류의 크기는 실효치가 사용되고 있으므로, 사인파 교류와 회전 벡터와의 사이에 다음과 같은 약속을 한다. 벡터의 크기 = 사인파 교류의 실효치 벡터의 편각 = 사인파 교류의 위상각 그림 1-2 벡터 그림의 예 예를 들면, ​ 의 사인파 교류를 벡터로 표현하면 ​ 가 된다. 이들 벡터 그림은 그림 2-2과 같이 된다. 2. 벡터와 복소수 교류는 벡터로 표현할 수 있었으나, X..

1. 전자 유도란? 그림 1-1과 같이 자석을 코일의 안에 집어넣은 순간, 코일에 연결된 검류계는 그림의 방향으로 지침이 흔들리고, 코일에는 전류가 흘러 코일의 양단에는 기전력이 생긴 것을 알 수 있다. 코일 안에 집어넣은 자석을 코일에서 꺼낸 순간에는 검류계가 역의 방향으로 흔들린다. 또한, 그림 1-1(b)에 있어서 철심에 감은 한 쪽의 코일에 스위치 S의 개폐에 의해 전류의 변화를 주면, 다른 쪽의 코일에 전류가 흐른다. 이와 같은 현상을 전자 유도라고 하고, 전자 유도에 의해서 발생한 전압을 유도 기전력, 흐르는 전류를 유도 전류라고 한다. 그림 1-1 전자 유도 여기에는 전자 유도에 관한 2개의 법칙이 있다. (1) 유도 기전력의 크기를 표현하는 패러데이의 법칙 유도 기전력의 크기는 코일을 관통..

1. 병렬 접속 두개 이상 저항을 병렬로 접속하는 것을 저항의 병렬접속이라고 한다. 예를 들면, 2개의 저항 R1,R2의 병렬 접속은 그림 1.1과 같이 단자 1과 단자 2, 그리고 단자 1'과 단자 2'를 함께 접속한 것이다. 2. 병렬 접속의 합성 저항 그림 1-2(a)는 n개의 저항 R1,R2,R3,···Rn을 병렬 접속하고, 이것에 전원의 전압 V[V]를 더한 회로이다. 같은 그림에 있어서, R1,R2,R3,···Rn에는 전압 V[V]가 그대로 가해지기 때문에, 각 저항에 흐르는 전류 I1,I2,I3, ···In은 다음과 같이 된다. 또한, 전원으로부터 흐르는 전체 전류 I[A]는 각 저항에 흐르는 전류의 합이기 때문에 다음에 그림 1-2(b)와 같이 1개의 저항 R[Ω]에 그림 (a)와 동일 전..

1. 직렬 접속 2개 이상 저항을 1렬에 접속하는 것을 저항의 직렬 접속이라고 한다. 예를 들면, 2가지의 저항 R1,R2의 직렬 접속은 그림 1.1과 같이 단자 1'와 2를 연결하여 1렬로 한 것이다. 그림 1-1 직렬 접속 (1) 그림 1-2 직렬 접속 (2) 그림 1-3(a)는 n개의 저항 R1, R2, R3, ···, Rn을 직렬 접속하고, 이것에 전원의 전압 V[V]을 더한 회로이다. 이 경우, 회로에 흐르는 전류는 전원으로부터 흘러나오는 전류도, R1,R2,R3,···,Rn의 저항을 흐르는 전류도, 전원으로 되돌아가는 전류도, 모두 동일 크기의 전류이다. 2. 직렬 접속의 합성저항 그림 1-3(a)에서, 전압 V[V]를 더한 때, 전류 I[A]가 흘렀다고 한다. 이 때, 각 저항의 양단의 전압..