1. 전자 유도란?
그림 1-1과 같이 자석을 코일의 안에 집어넣은 순간, 코일에 연결된 검류계는 그림의 방향으로 지침이 흔들리고, 코일에는 전류가 흘러 코일의 양단에는 기전력이 생긴 것을 알 수 있다. 코일 안에 집어넣은 자석을 코일에서 꺼낸 순간에는 검류계가 역의 방향으로 흔들린다. 또한, 그림 1-1(b)에 있어서 철심에 감은 한 쪽의 코일에 스위치 S의 개폐에 의해 전류의 변화를 주면, 다른 쪽의 코일에 전류가 흐른다.
이와 같은 현상을 전자 유도라고 하고, 전자 유도에 의해서 발생한 전압을 유도 기전력, 흐르는 전류를 유도 전류라고 한다.
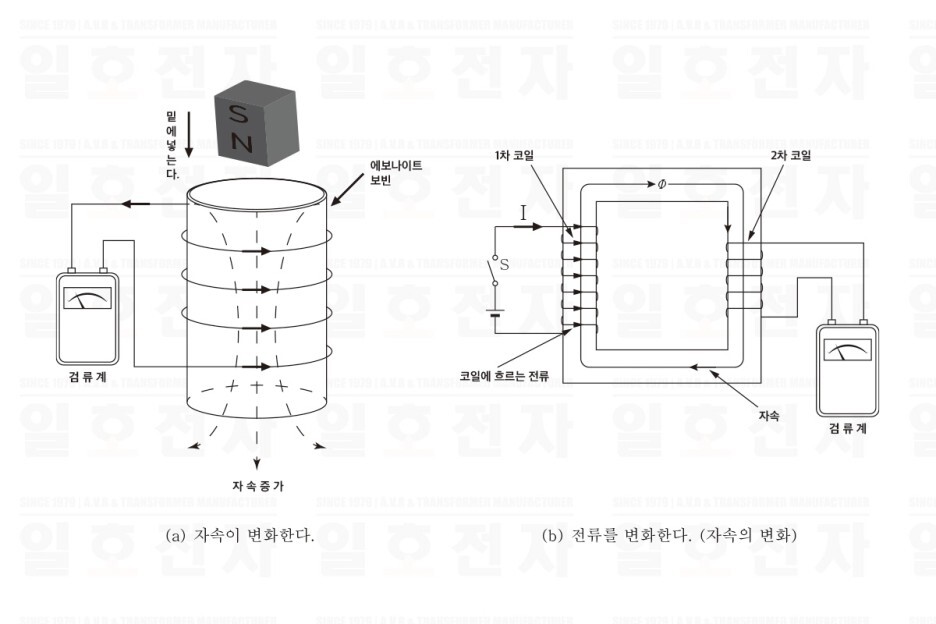
그림 1-1 전자 유도
여기에는 전자 유도에 관한 2개의 법칙이 있다.
(1) 유도 기전력의 크기를 표현하는 패러데이의 법칙
유도 기전력의 크기는 코일을 관통하는 자속의 시간에 대한 변화의 비율과 코일의 권수에 비례한다.
(2) 유도 기전력의 방향을 나타내는 렌쯔 법칙
유도 기전력의 방향은 유도 전류를 만드는 자속이 처음의 자속의 증감을 방해하는 방향에 생긴다.
2. 인덕턴스란
코일에 흐르는 전류가 변화하면 코일을 관통하는 자속이 변화하기 때문에 코일에는 기전력이 발생한다. 이와 같은 현상을 자기 유도라고 하고, 그 크기를 자기 인덕턴스로 표현한다. 또한 2개의 코일을 가까이 하고, 한 편의 코일에 전류를 변화시켜서 흐르게 하면 다른 편 코일에 기전력이 발생한다. 이와 같은 현상을 상호 유도라고 하고, 그 크기를 상호 인덕턴스로 표현한다.
(a) 자기 인덕턴스 그림 1-2에 있어서 권수 N회의 코일에 흐르는 전류 I가 Δt[s] 간에 ΔI[A] 변화하고, 코일 자신의 속을 관통하는 자속 φ가 Δφ[Wb] 변화하였다고 하면, 자기유도 기전력 e는 I전자 유도에 관한 2개의 법칙으로부터 다음과 같이 된다.
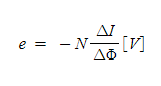
식 1-1
-는 자속의 변화를 방해하는 방향을 의미한다. 여기에서 철심이 갖는 투자율 μ의 값이 일정하면, 자속의 변화율 Δφ / Δt는 전류의 변화율 ΔI / Δt에 비례한다. 따라서, 비례 상수를 L이라고 하면, 자기 유도 기전력 e는 다음과 같이 된다.
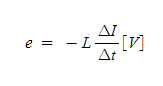
식 1-2
이 비례 상수 L은 코일의 형태, 권수, 크기, 자로의 투자율 등에 관계하는 특유한 양의 값으로 식(1-2)에서 L이 크면e도 커진다. 요컨데, L의 값은 코일의 자기 유도의 작용의 정도를 표현하게 되며, 이것을 자기 인덕턴스라고 한다.
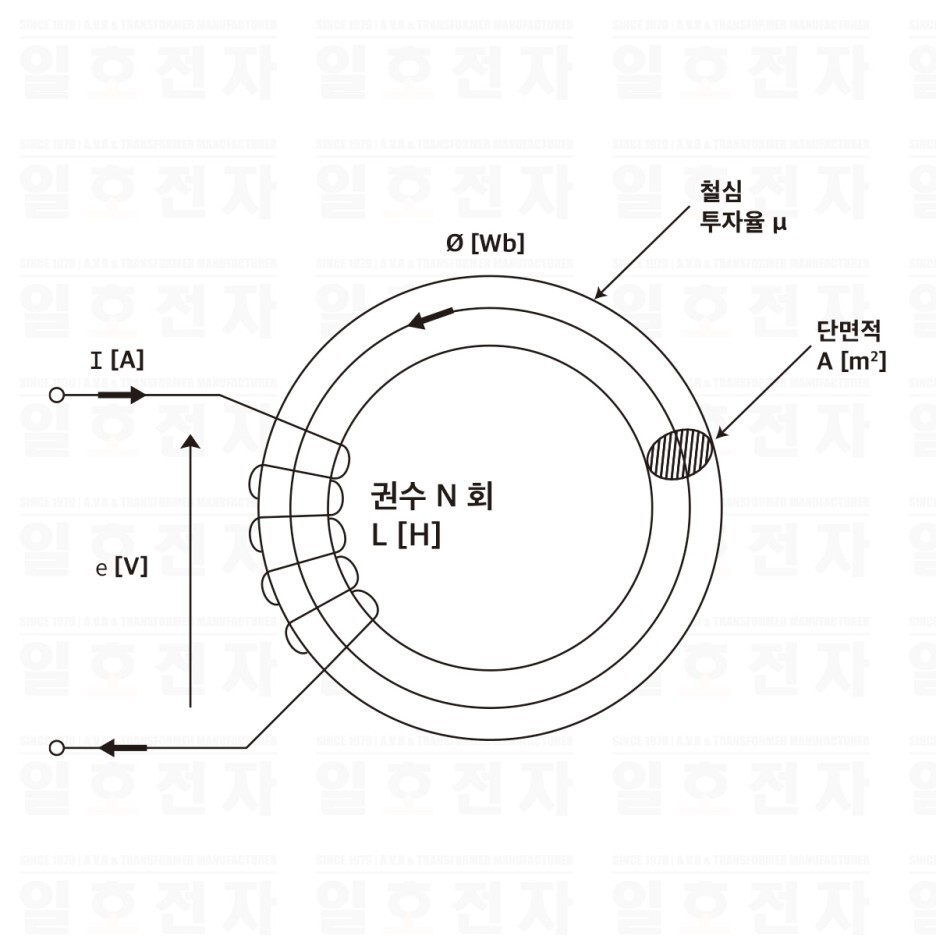
그림 1-2
자기 인덕턴스 L의 단위에는 헨리[H]를 사용한다. 1H의 10-3 QOFMF 1mH, 10-6배를 1μH라고 한다. 그런데 식 1-1과 식 1-2는 동등하기 때문에 다음과 같이 된다.
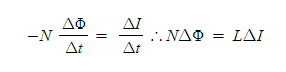
식 -13
그러므로, 자기 인덕턴스 L[H]는 코일에 I[A]의 전류가 흐를 때의 자속쇄교수 Nφ[Wb]를 알면 구할 수가 있다.
(b) 상호 인덕턴스 그림 1-4에 있어서 일차 코일에 전류를 흐르게 했을 때, 일차 코일의 전류 I가 Δt[s] 사이에 ΔI[A] 변화하였다고 하면, 2차 코일을 관통하는 자속 φ도 Δφ [Wb] 변화한다.
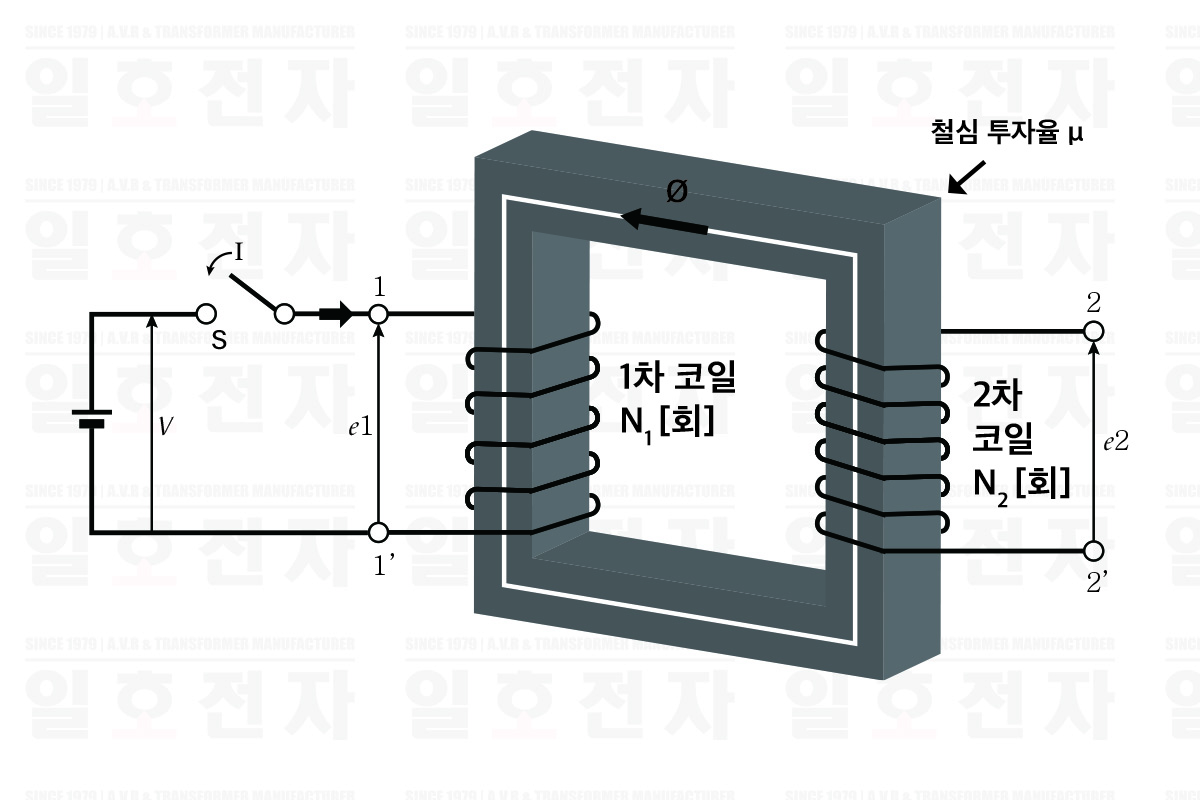
그림 1-3 상호 유도
따라서, 2차 코일의 권수를 N2로 하면, 2차 코일로 유도되는 기전력 e2(상호 유도기 전력)은 식 1-1과 마찬가지로 다음과 같이 된다.
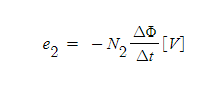
식 1-4
여기에서 투자율 μ가 일정하면, 자속의 변화율 Δφ / Δt는 전류의 변화율 ΔI / Δt에 비례하기 때문에 비례 상수를 M으로 하면, 기전력 e2는 다음과 같이 된다.
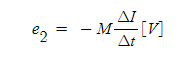
식 1-5
이 비례 상수 M은 2개의 코일 형태, 권수 상호 위치 등에 관계하는 특유한 양의 값이고 , 식(1-5)에서 M이 크면 e2 도 커진다. 따라서 M의 값은 상호 유도의 작용의 정도를 표현하게 되고, 이것을 상호 인덕턴스라고 한다. 또한, 식 1-4와 식 1-5에서 상호 인덕턴스 M은 다음과 같이 된다.
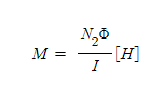
3. 코일의 접속
인덕턴스를 갖는 코일의 접속은 저항이나 콘덴서와 같이 직렬 접속, 병렬 접속이 있다. 표 1-1은 직렬 접속인데, 각 각의 코일에 의한 자속이 쇄교하지 않는 경우와, 쇄교하는 경우의 합성 인덕턴스이다. 또한 쇄교하는 경우는 한 편의 코일의 자속과 다른 편의 코일의 자속이 서로 합해지는 경우와, 쌍방이 반대가 되는 경우의 합성 인덕턴스는 달라진다. 표 1-2는 병렬 접속의 경우의 합성 인덕턴스이다.
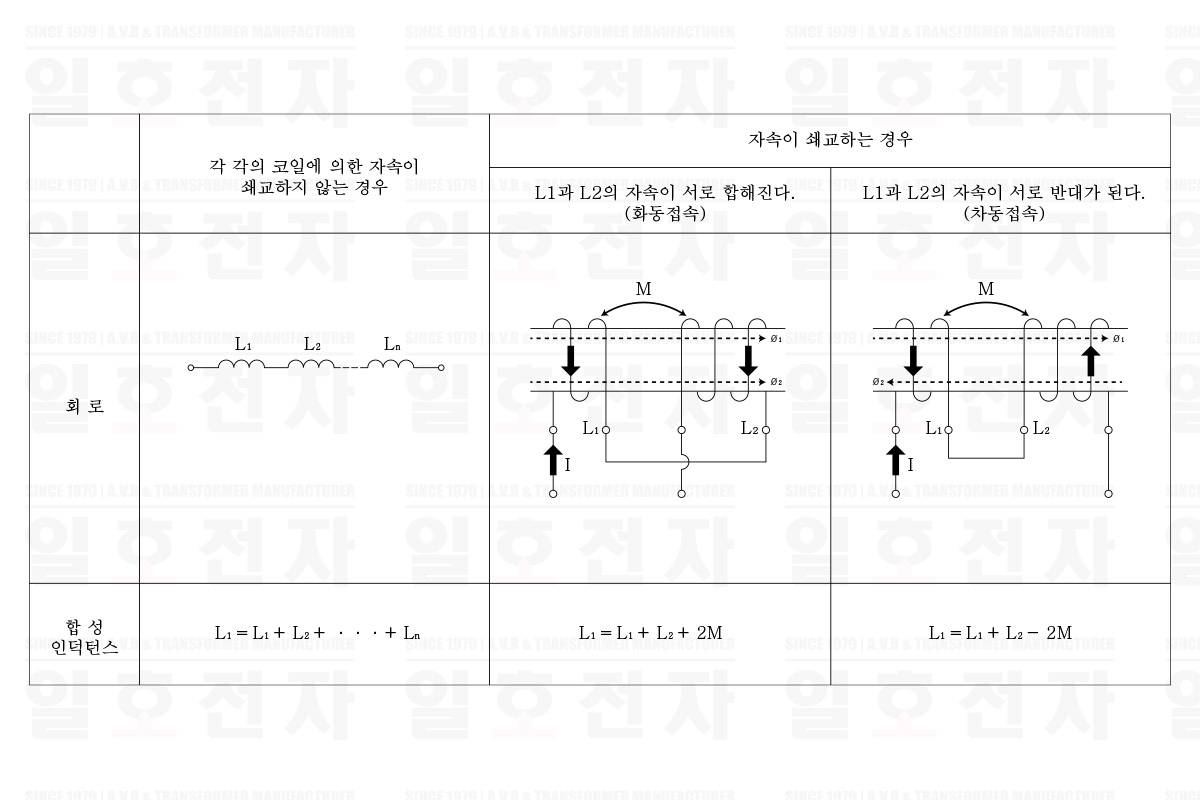
표 1-1 직렬 접속
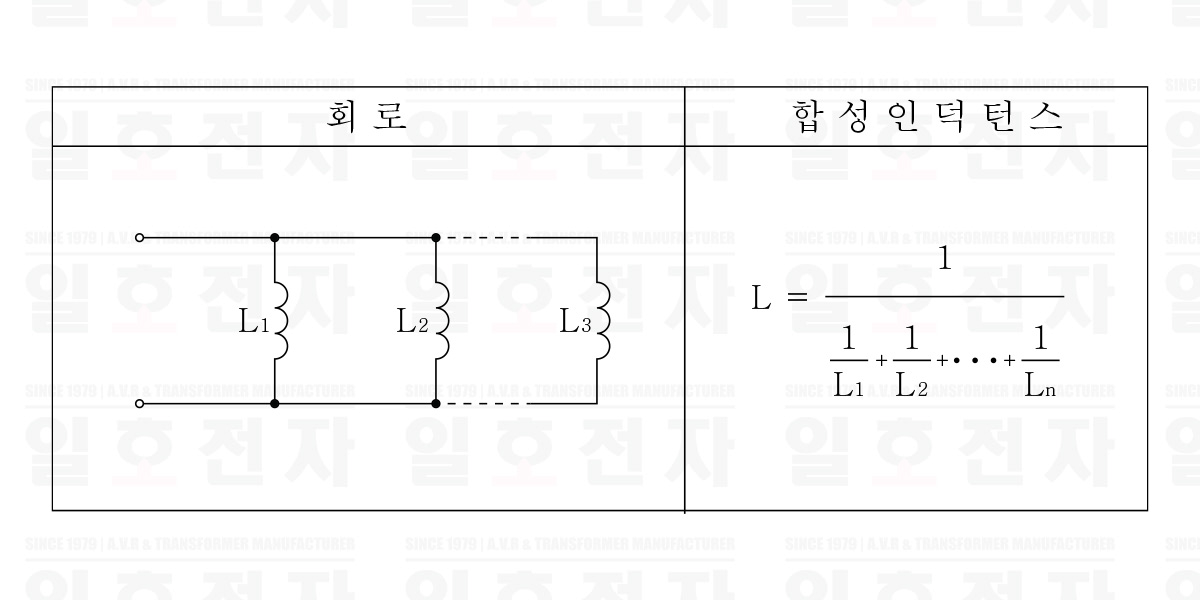
표 1-2 병렬 접속
'전기 전자의 기초 > 전자 회로의 이해하기 위한 직류 회로' 카테고리의 다른 글
| 1-6 정전 용량과 콘덴서의 접속 (0) | 2022.06.09 |
|---|---|
| 1-5 줄의 법칙과 전력. (0) | 2022.05.25 |
| 1-4 복잡한 회로의 전류를 구하는 방법. (0) | 2022.05.11 |
| 1-3 저항의 병렬 접속은 전류를 배분한다. (0) | 2022.04.20 |
| 1-2 저항의 직렬 접속은 전압을 배분한다. (0) | 2022.04.05 |